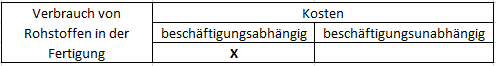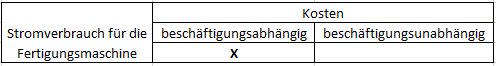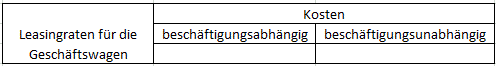Inhaltsverzeichnis:
Grundlagen Teilkostenrechnung
– Kostenarten
– Ermittlung von kv und KF
– Gewinnschwellenmenge
DB-1-Rechnung im 1- Produktunternehmen
– db und DB
– Zusammenhang db – KF und db – BE
– Einflussgrößen auf den xBEP
– kurz- und langfristige Preisuntergrenze
DB-1-Rechnung im Mehrproduktunternehmen
DB-2-Rechnung im Mehrproduktunternehmen
Engpassrechnung
Abkürzungsverzeichnis:
AK = AnschaffungsK
DB = Deckungsbeitrag
db = DB je Stück
EF = Eigenfertigung
eKF = erzeugnisfixe K
EKP = Einkaufspreis
FB = Fremdbezug
g = Stückgewinn
G = Gewinn
k = Stückkosten
K = Kosten
KF = Fixkosten
KV = variable Kosten
kv = variable k
naeKF=nicht abbaubare eKF
ND = Nutzungsdauer
NVKP = NettoVKP
pK = produktbezogene K
PUG = Preisuntergrenze
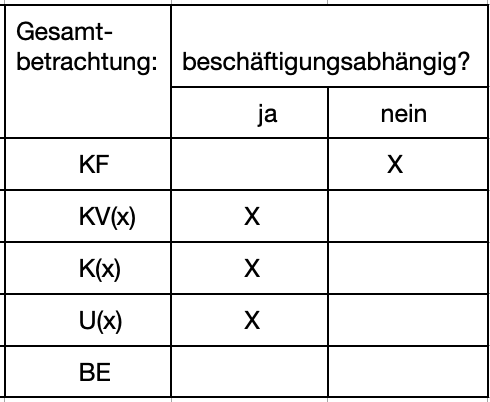
U = Umsatz
uKF = unternehmensfixe K
xBEP = break-even-point
Kostenarten
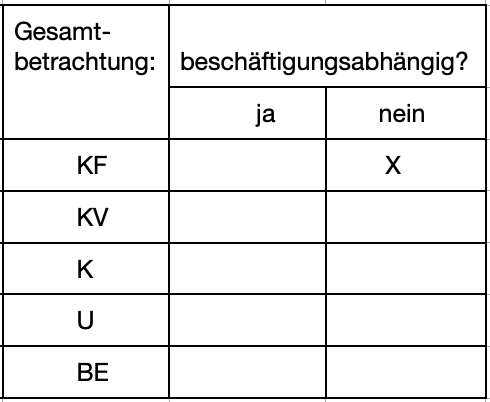
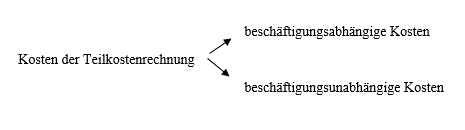
 Die Teilkostenrechnung unterscheidet zwischen beschäftigungsabhängigen
Die Teilkostenrechnung unterscheidet zwischen beschäftigungsabhängigen
und beschäftigungsunabhängigen Kosten.
Beschäftigungsunabhängige Kosten
 Unabhängig von der produzierten Menge fallen Fixkosten (KF) an.
Unabhängig von der produzierten Menge fallen Fixkosten (KF) an.
Damit sind die Fixkosten beschäftigungsunabhängige Kosten.
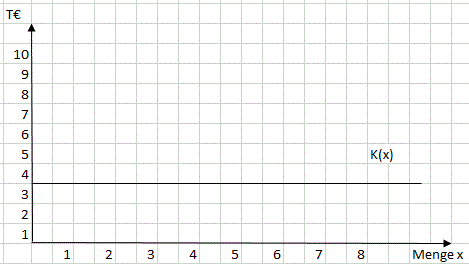
- Fixkosten (KF) tabellarisch:
>>>> KF tabellarisch: Vervollständigen Sie nachfolgende Tabelle.
- KF grafisch:
Kostenfunktion der PerKol Sportgeräte AG: KF = 3.000
Beschäftigungsabhängige Kosten

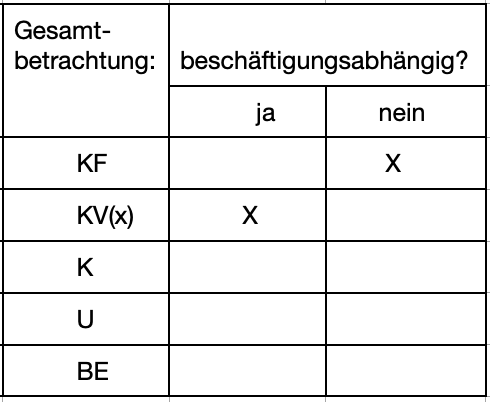
Beschäftigungsabhängige Kosten fallen nur an, wenn produziert wird.
Mit steigender Ausbringungsmenge steigen die gesamten variablen Kosten.
Mit fallender Ausbringungsmenge fallen die gesamten variablen Kosten.

Bei der PerKol Sportgeräte AG sind die variablen Kosten proportionale Kosten, d.h. die variablen Stückkosten sind konstant.
Mit jedem Stück, das zusätzlich produziert wird, kommen als zusätzliche variable Kosten die konstanten variablen Stückkosten dazu.
- variable Stückkosten (kv) und variable Gesamtkosten (KV) tabellarisch:
>> kv tabellarisch: Vervollständigen Sie nachfolgende Tabelle.
Unabhängig davon wieviel Stück produziert werden, pro Stück fallen immer konstant 500,00 € an variablen Stückkosten an.
>>>> KV tabellarisch: Vervollständigen Sie nachfolgende Tabelle.
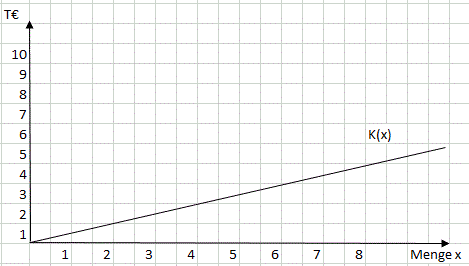
- variable Gesamtkosten grafisch:
Kostenfunktion allgemein: KV(x) = kv * x
Kostenfunktion der PerKol Sportgeräte AG: KV(x) = 500 * x
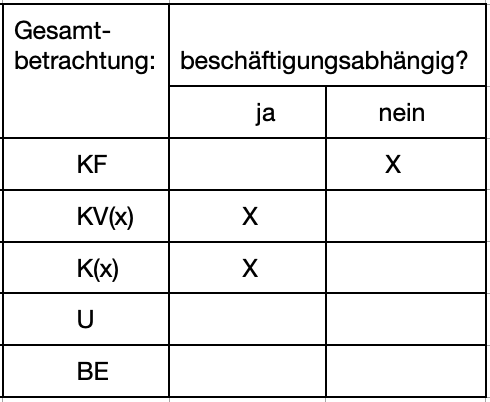
Gesamtkosten

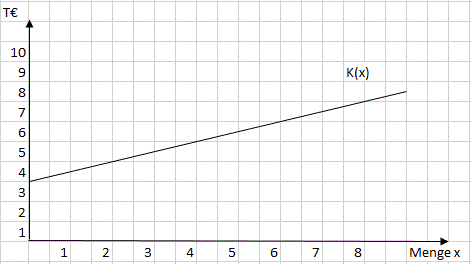
Gesamtkosten setzen sich aus beschäftigungsabhängigen Kosten und beschäftigungsunabhängigen Kosten zusammen.
K(x) = KF + kv * x
Allgemeine Kostenfunktion K(x) = a + m * x
x = Menge
a = y-Achsenabschnitt
m = Steigung des Grafen
Gesamtkostengleichung der PerKol Sportgeräte AG: K(x) = 3.000 + 500 * x
Übungen Kosten – Gesamt- und Stückbetrachtung
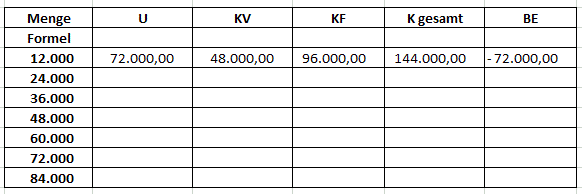
Übung 1: Gesamtbetrachtung – Umsatz, Kosten, Betriebsergebnis
Bei der PerKol Sportgeräte AG Werk 7 werden ausschließlich Gymnastikbänder produziert. Folgende Daten liegen vor:
- NVKP = 6,00 €
- kv = 4,00 €
- KF = 96.000,00 €
1.1 Vervollständigen Sie nachfolgende Tabelle und berechnen Sie in Abhängigkeit von der Ausbringungsmenge das erzielbare Betriebsergebnis:
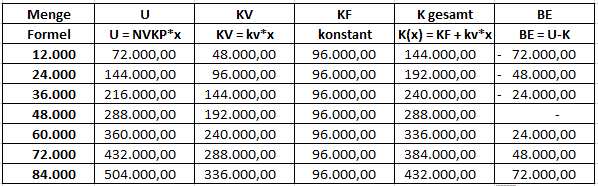
1.2 Erstellen Sie eine Grafik mit den Größen Umsatz, Kosten und Betriebsergebnis.
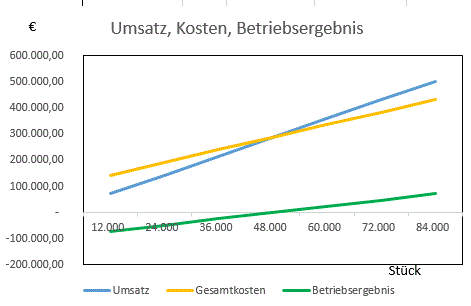
Übung 2: Stückbetrachtung: NVKP, k, g
2.1 Vervollständigen Sie nachfolgende Tabelle: KF = 96.000,00 €
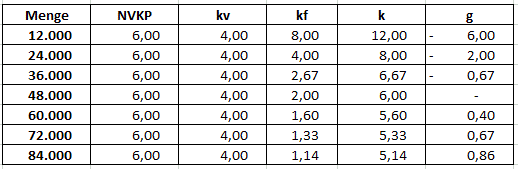
2.2 Erstellen Sie eine Grafik mit den Größen NVKP, Stückkosten k und Stückgewinn g.
>>>
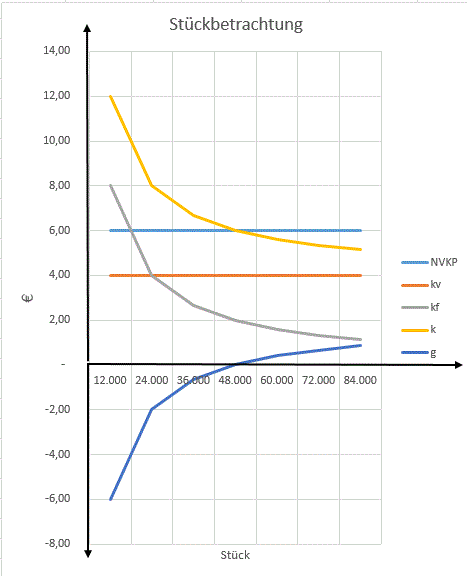
Werden 24.000 Stück produziert, betragen die Selbstkosten je Stck 8,00 €.
Werden 84.000 Stück produziert, betragen die Selbstkosten je Stck 5,14 €.
 Gesetz der Massenproduktion: mit zunehmender Produktionsmenge sinken die Stückkosten. Damit ist für die PerKol Sportgeräte AG als gewinnorientiertes Unternehmen ein erklärtes Ziel möglichst viel Produkte zu produzieren und zu verkaufen.
Gesetz der Massenproduktion: mit zunehmender Produktionsmenge sinken die Stückkosten. Damit ist für die PerKol Sportgeräte AG als gewinnorientiertes Unternehmen ein erklärtes Ziel möglichst viel Produkte zu produzieren und zu verkaufen.
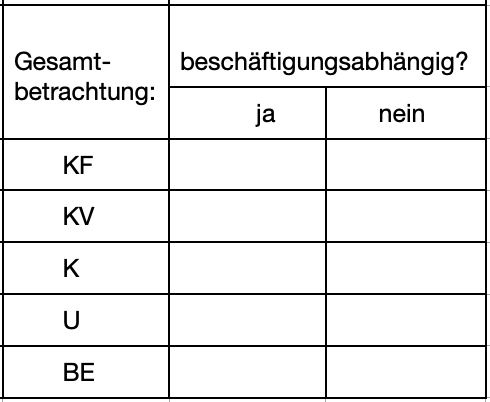
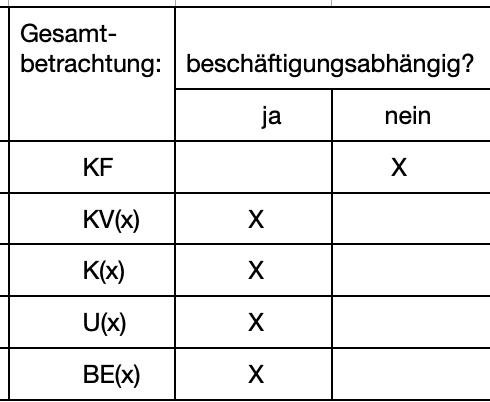
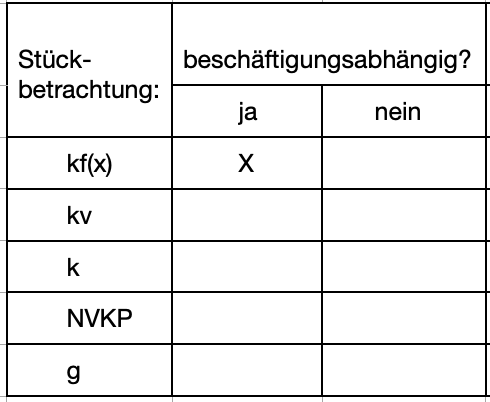
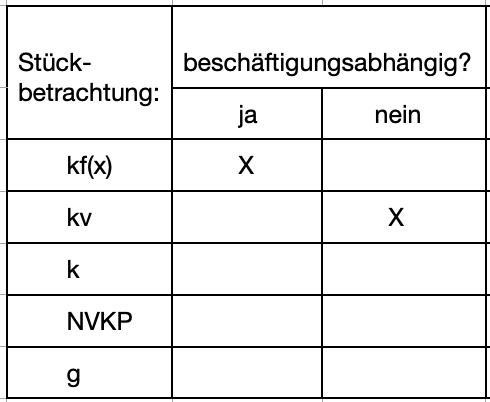
Beschäftigungsabhängige und beschäftigungsunabhängige Größen im Überblick
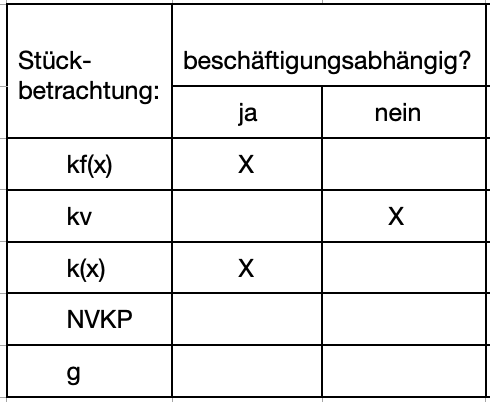
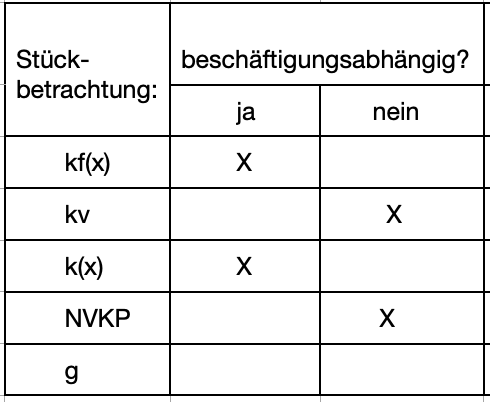
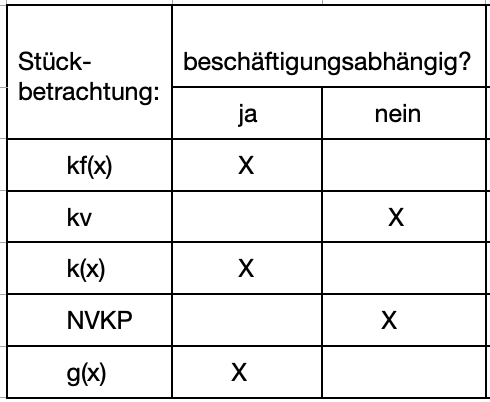
>>>> Entscheiden Sie jeweils, ob es sich um beschäftigungsabhängige Kosten handelt. Gesamtbetrachtung:
>>>> Entscheiden Sie jeweils, ob es sich um beschäftigungsabhängige Kosten handelt. Stückbetrachtung:
Schreibweise für beschäftigungsabhängige Größen:
Nicht BE = 5.000,00 €, sondern BE (2.000) = 5.000,00 €
Nicht K = 12.000,00 € , sondern K (4.000) = 12.000,00 €
Nicht g = 3,00 €/Stck., sondern g (20.000) = 3,00 €/Stck.
Beschäftigungsabhängige Kosten verändern sich in Abhängigkeit von der Menge.